レイと平面の当たり判定

レイと平面の当たり判定をする必要があったので、どのように考えたのかをメモ。（正しいかどうかはわかりません）

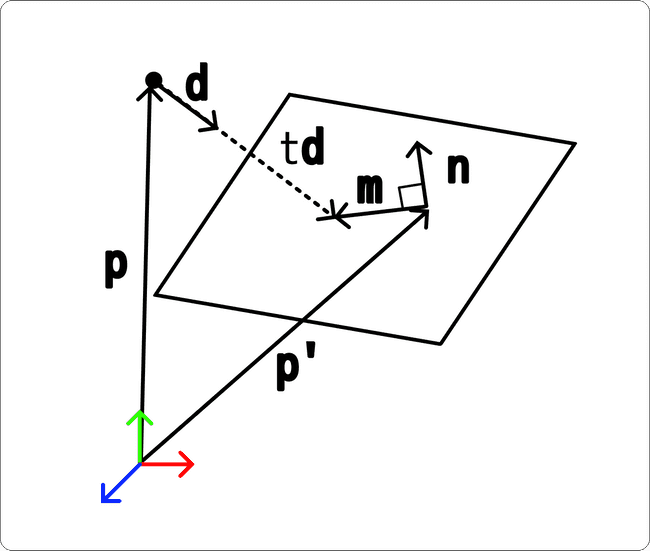
位置 $\bm{p}$、方向 $\bm{d}$ で表されるレイが、ある点 $\bm{p'}$ を通り、法線 $\bm{n}$ で示される平面を通過する地点までの距離 $t$ を求めるものとします。

$\bm{p'}$ からレイが衝突する地点までのベクトル $\bm{m}$ と法線ベクトル $\bm{n}$ のなす角は直角になるはずなので、以下の式が成り立ちます。

このとき、図の通り $\bm{m} = \bm{p'} - (\bm{p} + t \bm{d})$ で表せるので、

となり、これを 内積計算の分配法則などを利用して 変形していくと、

さらに整理して、

となります。この $t$ がレイの始点から平面までの距離となり、衝突位置は $\bm{p} + t\bm{d}$ で求めることができます。

なお、この式の分母 $\bm{n} \cdot \bm{d}$ が 0 になる場合は $t$ の値を求めることはできませんが、この場合は面の法線ベクトルとレイの方向ベクトルが直交することになるので、レイと平面が平行ということになり、交わる点がないということを表しています。