三次元空間上の道路どうしを接続できるようにする

前回の記事に引き続き、道路を敷設するためのあれこれをつくっていますが、今回は道路同士の接続について考えてみます。

構成

道路オブジェクトは二つの端点を持ち、それぞれにハンドルが割り当てられています。マウスでハンドルをつかむと、地面上を移動させることができます。

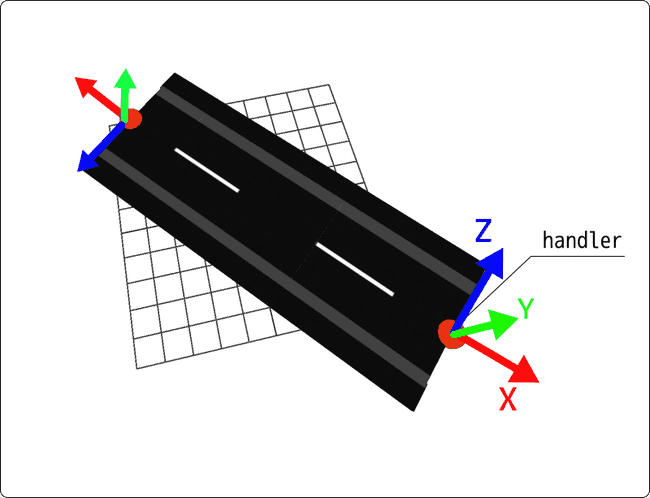
ハンドルと同じ位置に道路の端点があります。図に示すようにX軸が道路の外側を向き、Y軸が上方向に向くように座標系が割り当てられています。

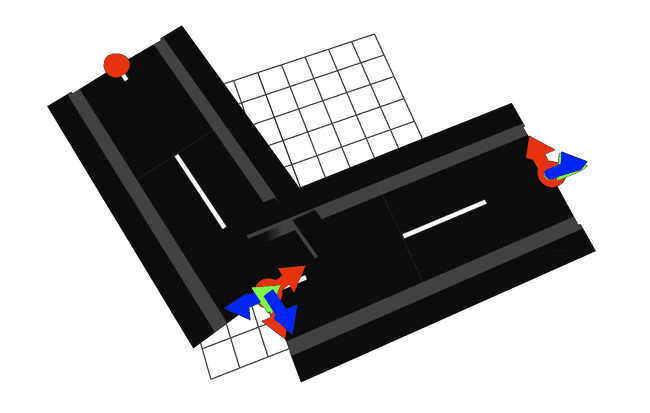
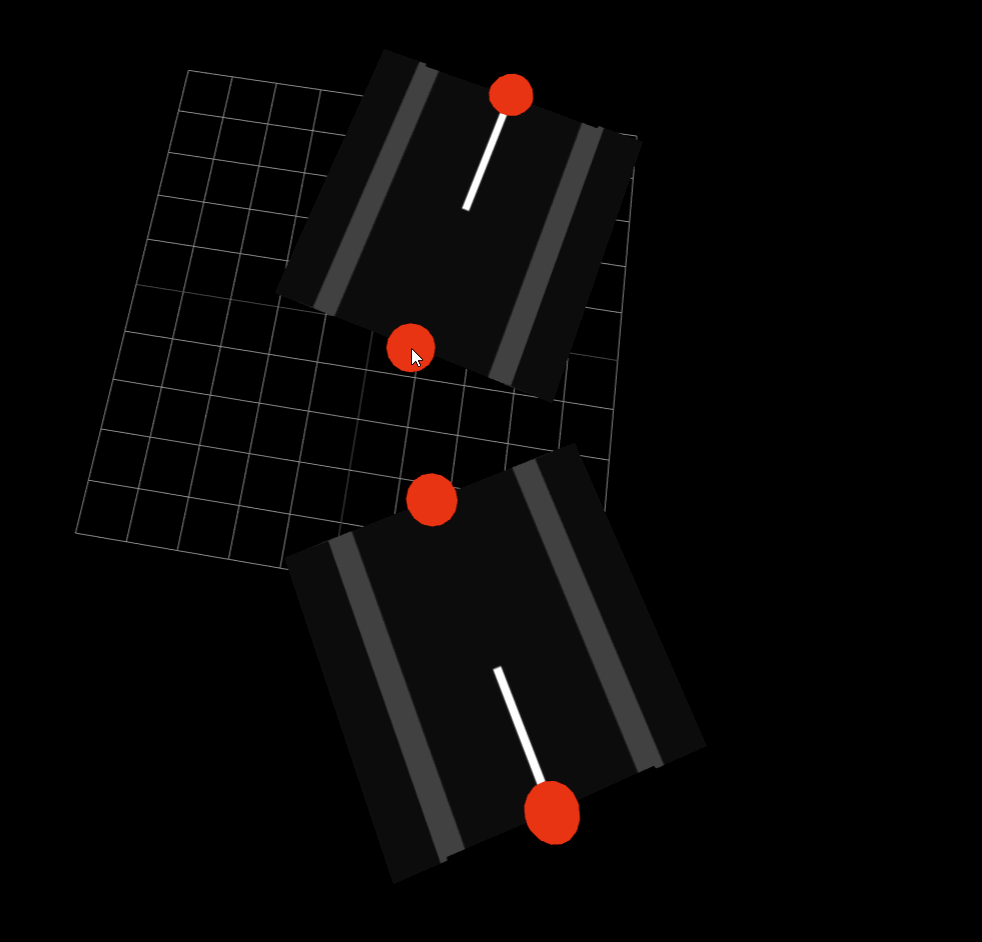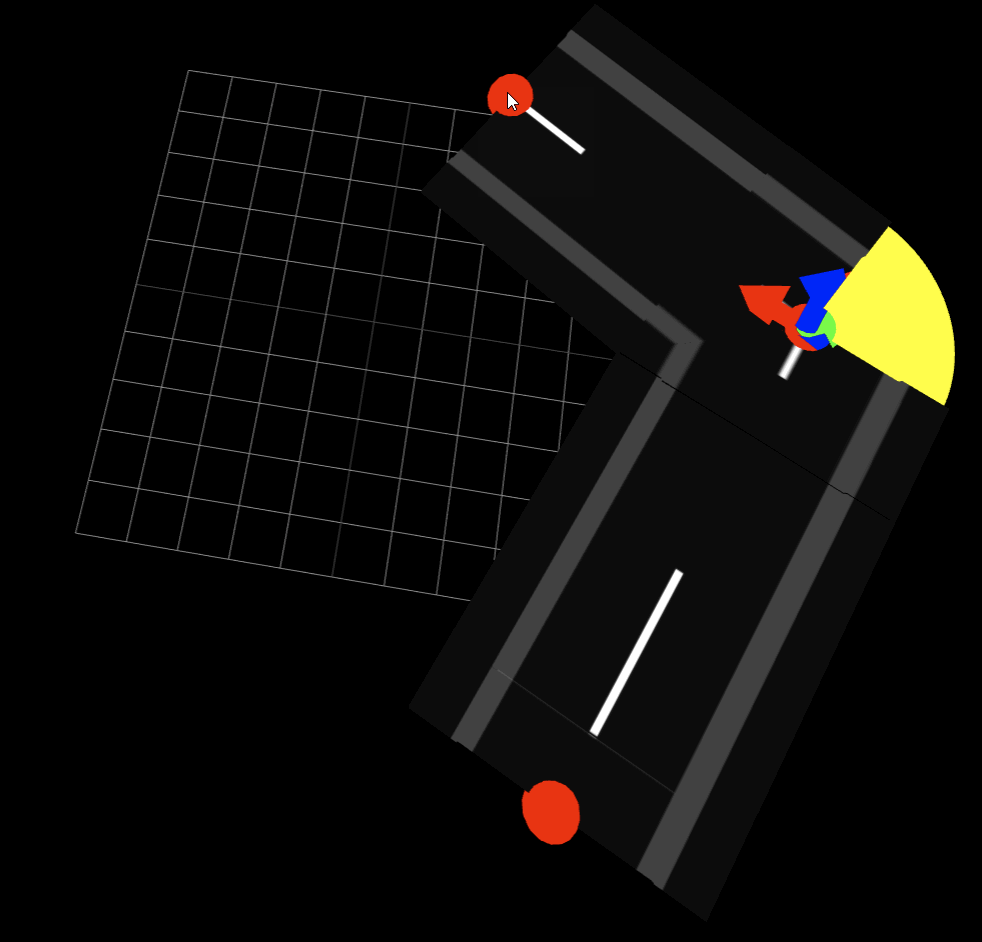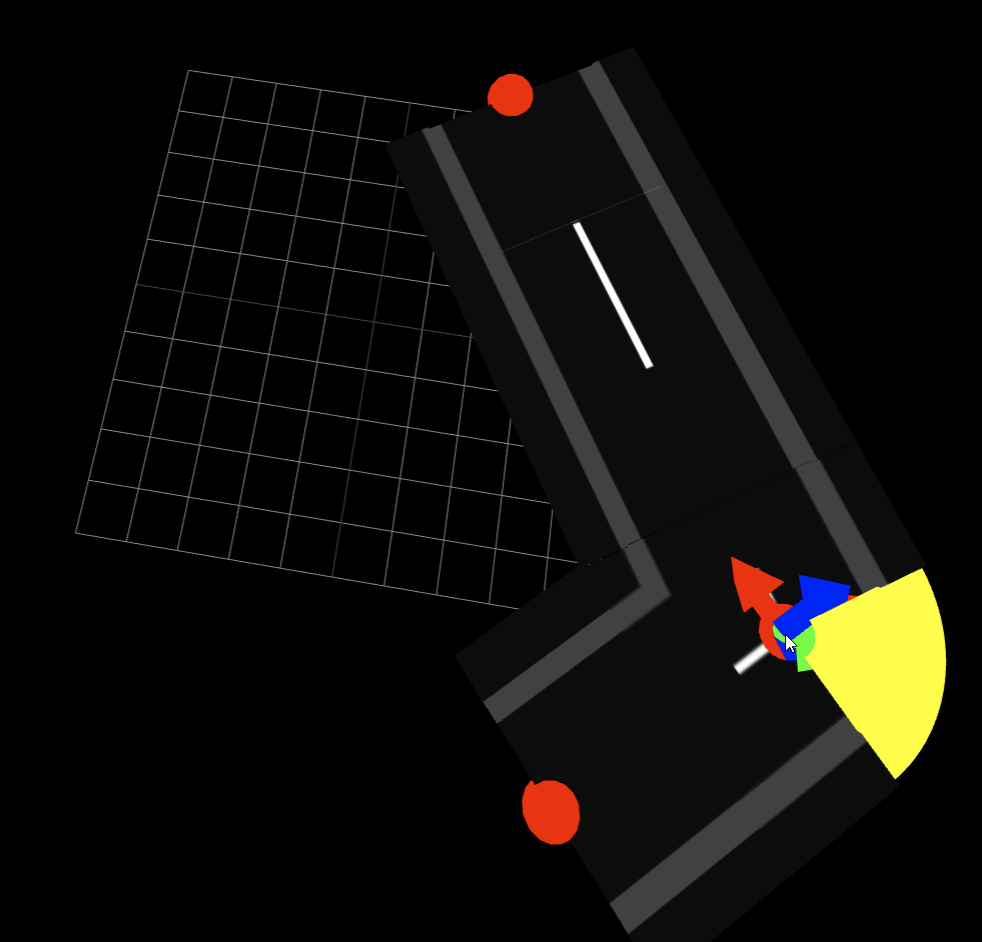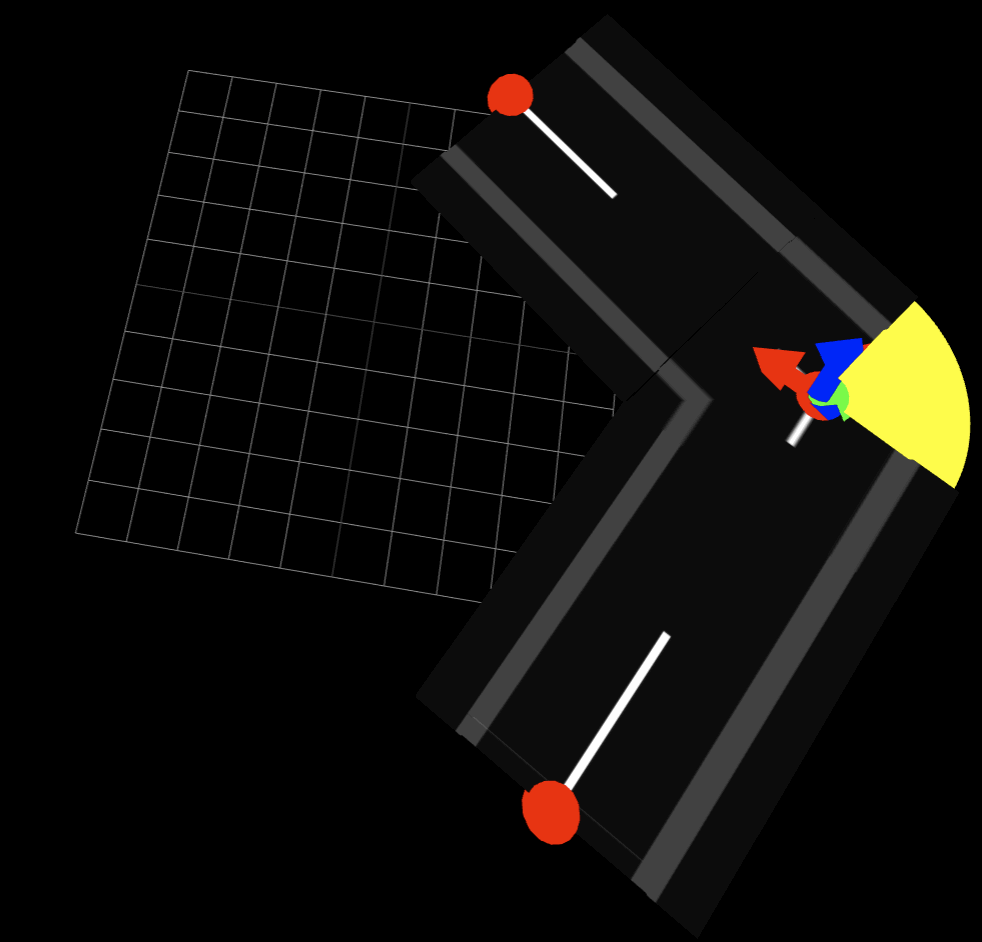
道路の端点同士の処理が行われないまま二つの道路を接続しようとすると、このように道路同士が重なってしまいます。

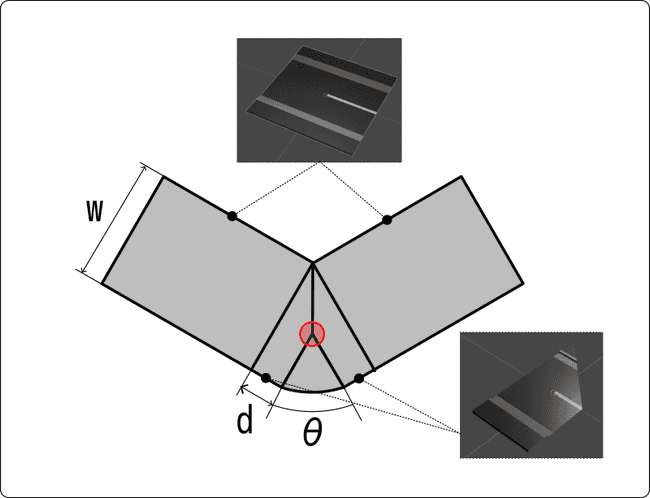
そこで、このように端点付近のパーツをいくつかに分けます。 道幅 $w$ の道路に対して、図に示される角度 $\theta$ と距離 $d$ を求めれば、それぞれのパーツの大きさを決定できそうです。

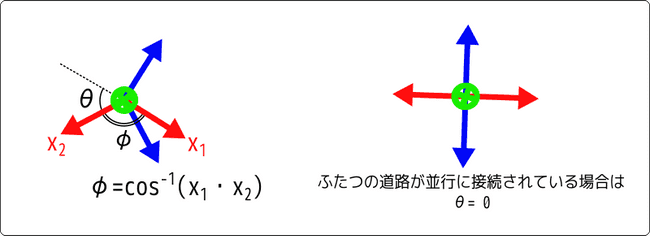
角度 $\theta$ については、道路の端点に割り当てられた座標軸のなす角 $\phi$ を求めることで計算できます。 座標軸 $x_1$, $x_2$ の長さが1とすれば、内積の式より $\phi = cos^{-1}(\bm{x_1} \cdot \bm{x_2})$ で計算できます。 二つの道路が完全に平行の場合は $\phi = \pi$であることを考慮すると、$\theta = \pi - \phi$ で算出されます。

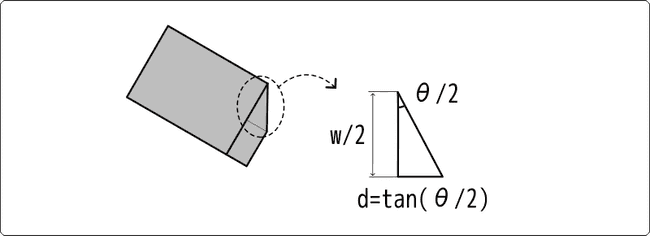
つぎに $d$ を求めます。図の一部を切り出して確認していくと、角度 $\frac{\theta}{2}$、高さ $\frac{w}{2}$ の直角三角形がとれます。 この三角形の高さ $tan(\frac{\theta}{2})$ が求めるべき $d$ の値になります。

というわけで、まとめると以下のようになります。

描画

各パーツのサイズが計算できたので、描画する方法を考えます。

直線パーツの描画

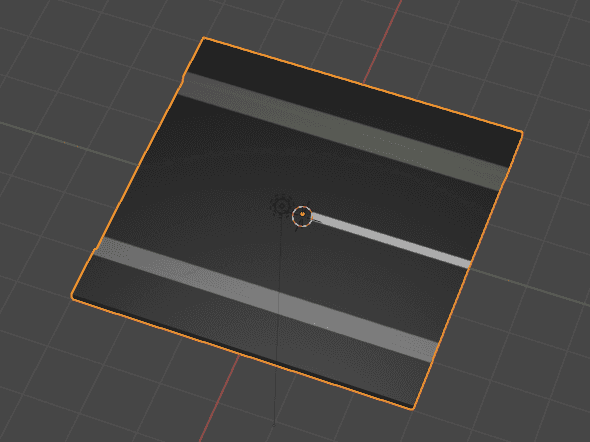
上図のような単位長さのパーツをモデリングツールで作っておき、縦方向（X軸方向）に拡大（あるいは縮小）することで描画します。道路オブジェクトの座標系を表す行列に拡大行列を掛けることでこれを行います。 three.js であれば、Object3D.scale を使うことでこれを行うことができます。

ただ単に拡大すると、テクスチャも一緒に引き伸ばされてしまいますので、テクスチャをリピートされるようにします。three.jsなら Texture.repeat を使ってテクスチャのリピート数（何度テクスチャを繰り返し描画するか）を指定できます。

const material = new MeshStandardMaterial()

// ... テクスチャをロードする ...

// 単位長さのパーツの拡大率を計算する
// length: 直線パーツの長さ, renderingObjectSize: 単位長さのパーツの長さ
const itemScale = length / renderingObjectSize

// 長さ方向のテクスチャのリピート数を設定する
material.map.repeat.x = itemScale

端点パーツの描画

図のような基本パーツをモデリングツールで作っておき、縦方向（X軸方向）に拡大縮小することで描画します。

コーナー部分の描画

角度 $\theta$ によってメッシュの形を変える必要があるので、円形メッシュを動的に生成することにしました。three.js の CircleGeometry を使って描画します。

※ 筆者は既存のメッシュの頂点をうまく調整する方法を知らないので、これまでのようにメッシュをモデリングツールであらかじめ作っておくのではなく基本図形を使って生成することにしましたが、もし「こうやるといいよ！」という情報をお持ちでしたら@piyorinpaまで教えてください🙏

ここまで実装すると以下のようになります。黄色い部分には後程テクスチャを貼る予定。

まとめ

とりあえずファーストステップとして道路同士を接続することができました。これを三叉路以上の交差点に応用し、いいかんじに道路を敷設できるようにしていきます。ではでは～