2点間の線分上に点が存在することを確認したい

いまつくっているアプリケーションに必要な「線分上に点が存在するかどうか」を確認する処理を考えます。

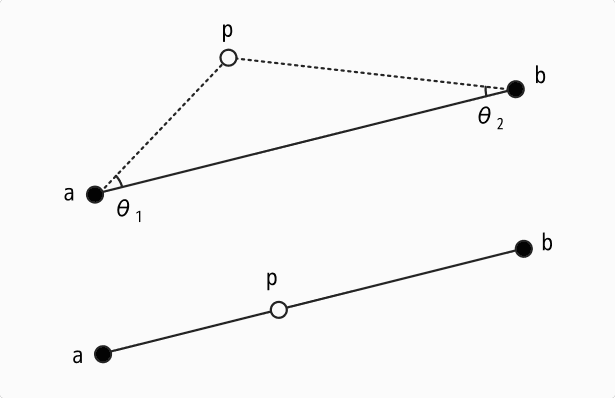
線分の上に点が存在する場合、点と線分の端点を結ぶ直線と、線分のなす角度 $\theta_1$, $\theta_2$ は0°になります。

角度を計算するには内積を利用できそうです。

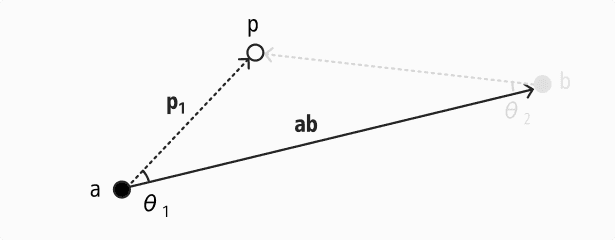
まずは端点から点にのびるベクトル $\bm{p_1}$ と、線分のベクトル $\bm{ab}$ を考えます。 このとき、先ほどの内積の公式を用いて、$cos\theta_1$ を計算できます。

この$cos\theta_1$が1に近ければ、$\theta_1$は0°に近いと言えます。

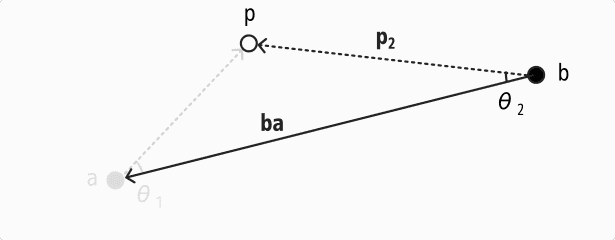
同様に、$cos\theta_2$も計算します。$cos\theta_1$もしくは$cos\theta_2$のどちらかが1に近ければ(=どちらかの角度が0に近ければ)線分上に点があると言うことができそうです。

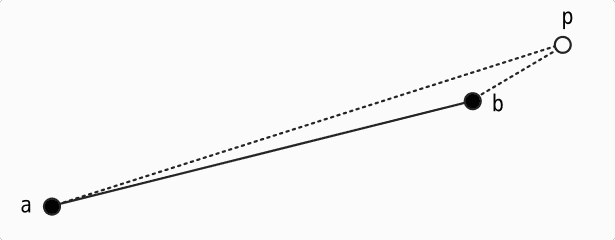
ただし、$cos\theta_1, cos\theta_2$いずれの値も正でなければ、線分の外側の直線上に点が存在することになります。

TypeScriptで実装した場合、最終的には以下のようなコードになりました。

type Position2D = [number, number]

const subtract = ([ax, ay]: Readonly<Position2D>, [bx, by]: Readonly<Position2D>): Position2D => [ax - bx, ay - by]
const length = ([x, y]: Readonly<Position2D>): number => Math.sqrt(x * x + y * y)
const innerProduction = ([ax, ay]: Readonly<Position2D>, [bx, by]: Readonly<Position2D>): number => ax * bx + ay * by

function pointInLine(a: Position2D, b: Position2D, point: Position2D) {
  // 線分の端点1から点に向かって伸びるベクトルp1
  const p1 = subtract(point, a)
  // p1の長さ
  const lp1 = length(p1)
  // 線分の端点1からもう一方の端点に向かって伸びるベクトルab
  const ab = subtract(b, a)
  // p1とabのなす角 (cos)
  const angle1 = innerProduction(ab, p1) / (length(ab) * lp1)
  
  // p2もp1と同様に計算する
  const p2 = subtract(point, b)
  const lp2 = length(p2)
  const ba = subtract(a, b)
  const angle2 = innerProduction(ba, p2) / (length(ba) * lp2)
  
  return (angle1 > 0) && (angle2 > 0) &&    // cos()の値が正であれば点は線側にある
    (Math.max(angle1, angle2) > 0.999)      // どちらかのcos()の値がほぼ1 -> 角度は0
}

おおむねこんなかんじでしょうか。ではでは。