画面座標からカメラの位置姿勢を考慮したレイ（半直線）を生成する

November 23, 2022

久しぶりの最近の開発の記録のようすです。ここ最近は3Dプログラミングの習得もかねて、3D空間に道路を敷設するプログラムをずっと書いてました。（3次元空間に自由に街っぽい空間を作れたら楽しいだろうなと思ったので、このようなアプリケーションをつくることを目指してみています。）

このように、ある平面上に道路を敷設することを考えます。「どこに道路を敷設するか」をマウスカーソルで指示することになりますが、今回の記事で説明する「カーソル位置からレイを生成」し、「レイと平面の当たり判定を行う」ことでこれを実現します。

※筆者は3Dプログラミングについて学習中の身であるため、解説内容が正確でない可能性があります。ご自身で補足資料を用意したりしながら話半分で見ていただけますとです。書籍実例で学ぶゲーム3D数学がおすすめです。

クリックされたカーソル位置から3次元空間上にレイを生成する

画面に映っている平面をクリックしたとき、平面のどこをクリックされたかを知る必要があります。画面をクリックしてカメラの姿勢に対応したレイ $\bm{d}$ （=半直線）を知ることができれば、以前実装した「レイと平面の当たり判定」を用いてこれを実現することができそうです。

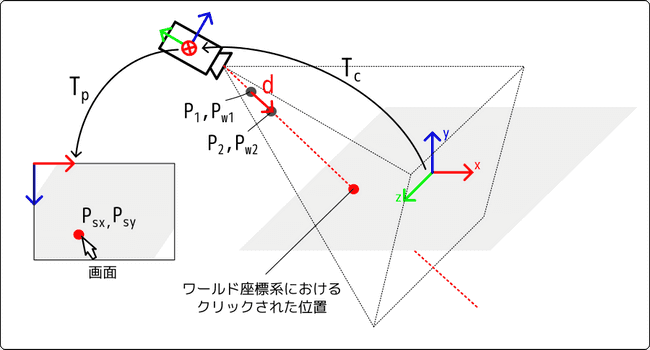
マウスカーソルのスクリーン座標からレイを作成します。透視投影行列の逆行列を利用して、スクリーン座標系からカメラ座標系における位置 $\bm{P_1}$ を求めます。

透視投影行列の逆行列 $\bm{T_p^{-1}}$ 、スクリーン座標系のカーソル位置 $p_{sx}$ 、 $p_{sy}$ （ $0 \leq p_{sx} \leq 1$ , $0 \leq p_{sy} \leq 1$ ）として、透視投影変換後の座標系の奥行成分が1のときの座標を求めます。

\bm{P_1'} = \begin{pmatrix} p_{sx} \\ p_{sy} \\ 1 \\ 1 \\ \end{pmatrix}\bm{T_p^{-1}}

計算された $\bm{P_1'}$ の4行1列目の成分(w)でほかの成分を除算して、 $\bm{P_1}$ を求めます。（4次元座標のw成分を 1 にするような座標が3次元上の空間の座標と一致するという理解（なのでwで割る）。たとえば透視投影変換を行うと、この成分が 1 以外の値をとるようになり、これが視錐台の奥行方向に応じた点の位置に影響する）

\bm{P_1} = \begin{pmatrix} p'_{11} \\ p'_{12} \\ p'_{13} \\ \end{pmatrix} \frac{1}{p'_{14}}

さらに、ワールド座標系-カメラ座標系の変換行列 $\bm{T_c}$ を用いて、 $\bm{P_1}$ のワールド座標系 $\bm{P_{w1}}$ を求めます。

\bm{P_{w1}} = \bm{P_c} \bm{P_1}

同様にもう1点 $\bm{P_w2}$ を求めます。今度は透視投影変換後の座標系の奥行成分が0.9のときの座標を求めます。

\bm{P_2'} = \begin{pmatrix} p_{sx} \\ p_{sy} \\ 0.9 \\ 1 \\ \end{pmatrix}\bm{T_p^{-1}}, \bm{P_2} = \begin{pmatrix} p'_{21} \\ p'_{22} \\ p'_{23} \\ \end{pmatrix} \frac{1}{p'_{24}}, \bm{P_{w2}} = \bm{P_c} \bm{P_2}

2点間を結ぶ方向ベクトルを正規化して作った方向ベクトルをレイとします。

\bm{d} = \frac{\bm{P_{w2}} - \bm{P_{w1}}}{|\bm{P_{w2}} - \bm{P_{w1}}|}

位置 $\bm{P_{w1}}$ と方向 $\bm{d}$ で表現されるレイを用いてレイと平面の当たり判定を行い、三次元ワールド空間の編集面上のどこをクリックしているかを判定できるようになりました。関連するソースコードは（このへん）にあります。

マウスカーソルの位置からワールド座標を得られることで、ある平面に平行な道路を引くための位置を画面から指示できるようになりました。

ということでひきつづき開発を頑張っていこうと思います。ではでは～。

🌟

...0

このカウンタは @piyoppi/counter-tools を使っています。

クリックすると匿名でいいねできます。